Вопросы:

1. Определение вектора. Основные понятия.
2. Линейные операции над векторами и их свойства.
3. Проекция вектора на ось. Основные свойства.
4. Линейная комбинация векторов. Понятие базиса на плоскости и в пространстве.
5. Понятие системы координат. Разложение вектора по ортам координатных осей.
6. Модуль вектора. Направляющие косинусы.
7. Действия над векторами, заданными своими координатами.
8. Скалярное произведение векторов. Определение и основные свойства.
9. Выражение скалярного произведения векторов через их координаты.
10. Векторное произведение двух векторов. Определение и основные свойства.
11. Выражение векторного произведения векторов через их координаты.
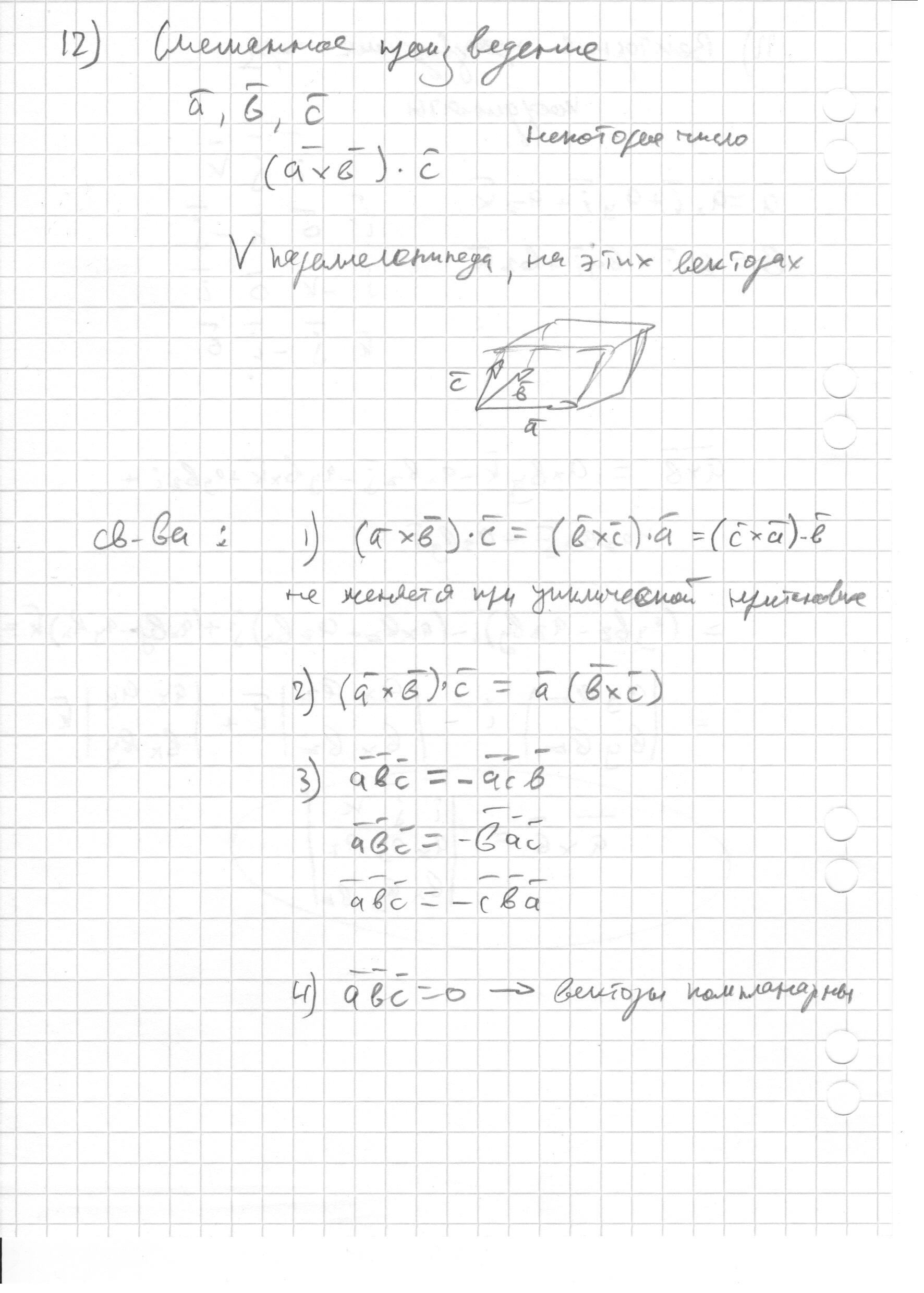
12. Смешанное произведение трех векторов. Определение и основные свойства.
13. Выражение смешанного произведения векторов через их координаты.
14. Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору. Общее уравнение плоскости.
15. Уравнение плоскости, проходящей через три точки.
16. Уравнение плоскости в отрезках. Нормальное уравнение плоскости. Преобразование общего уравнения плоскости к нормальному виду.
17. Расстояние от точки до плоскости.
18. Угол между двумя плоскостями. Взаимное расположение двух плоскостей в пространстве. Уравнение пучка плоскостей.
19. Прямая в пространстве. Векторное уравнение прямой. Параметрические уравнения прямой.
20. Канонические уравнения прямой. Уравнения прямой, проходящей через две точки.
21. Общие уравнения прямой. Преобразование общих уравнений прямой к каноническому виду.
22. Угол между прямыми. Взаимное расположение прямых в пространстве.
23. Условие, при котором две прямые лежат в одной плоскости.
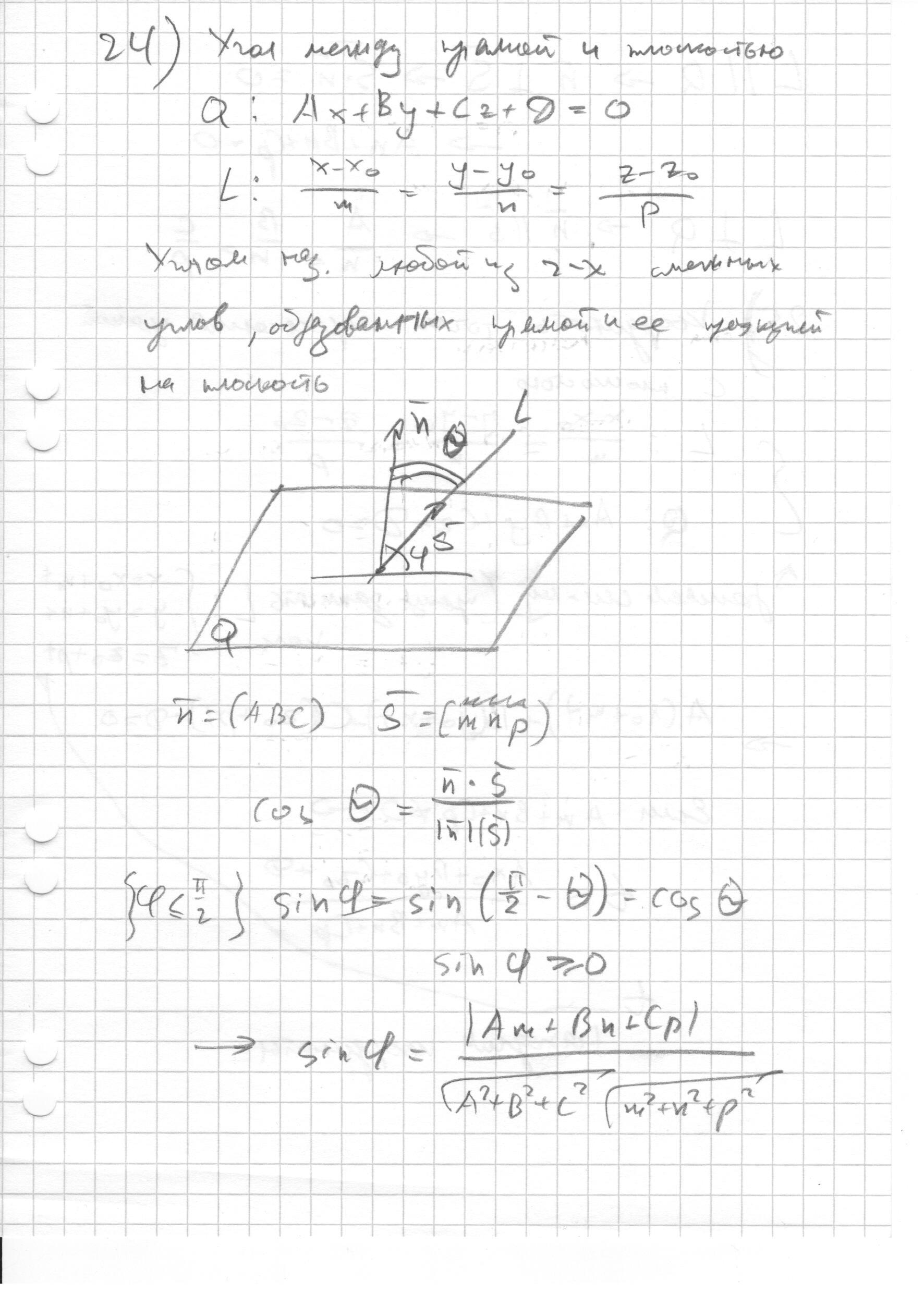
24. Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости.
25. Задача о вычислении координат точки пересечения прямой с плоскостью.
26. Условие принадлежности прямой плоскости.
27. Задача о вычислении расстояния от точки до прямой в пространстве.
28. Задача о вычислении кратчайшего расстояния между скрещивающимися прямыми в пространстве.
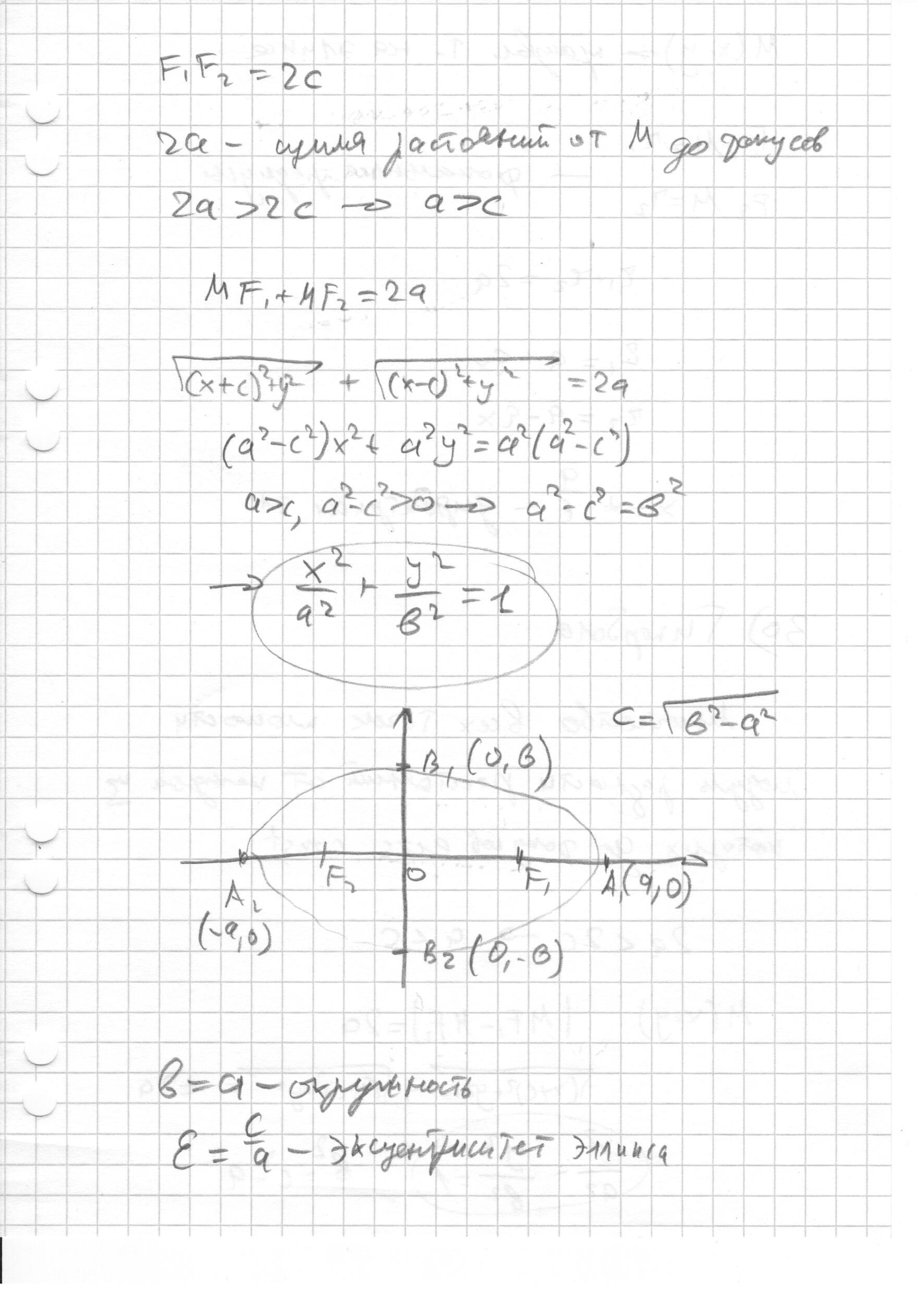
29. Эллипс. Определение, рисунок и основные понятия.
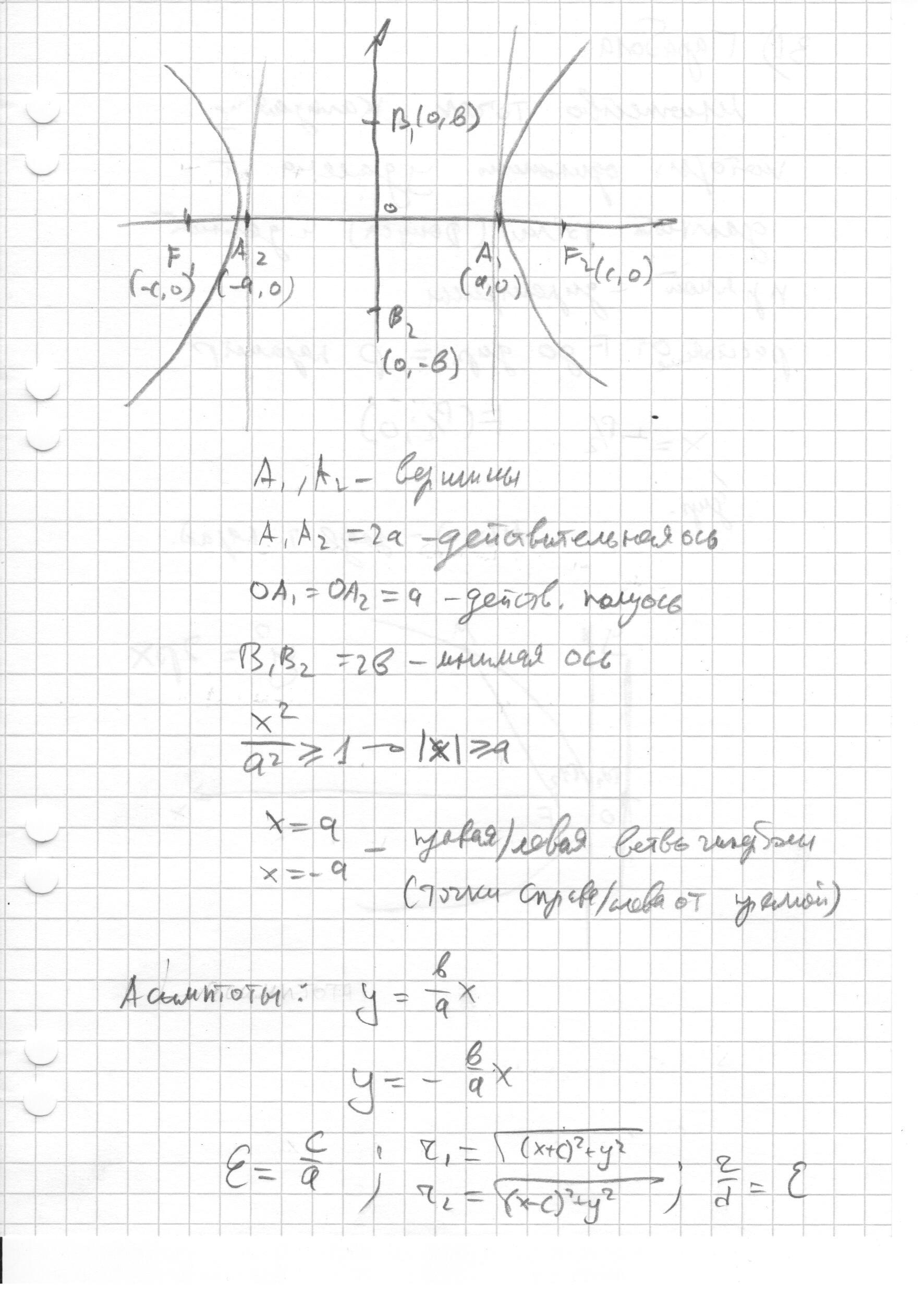
30. Гипербола. Определение, рисунок и основные понятия.
31. Парабола. Определение, рисунок и основные понятия.
32. Определители n-го порядка и их основные свойства. Минор и алгебраическое дополнение.
33. Матрица. Определение, основные виды матриц.
34. Линейные операции над матрицами и их основные свойства.
35. Произведение матриц. Определение и основные свойства.
36. Обратная матрица. Определение и основные свойства.
37. Вычисление обратной матрицы.
38. Решение СЛАУ с квадратной невырожденной матрицей коэффициентов с помощью формул Крамера.
39. Решение СЛАУ с квадратной невырожденной матрицей коэффициентов с помощью обратной матрицы.
40. Ранг матрицы. Элементарные преобразования матрицы.
41. Линейная зависимость системы столбцов. Основные теоремы об их линейной зависимости и независимости.
42. Теорема о ранге матрицы.
43. Теорема о базисном миноре.
44. Условие совместности и несовместности СЛАУ. Теорема Кронекера-Капелли.
45. Общее решение однородной СЛАУ, базисные и свободные неизвестные.
46. Фундаментальная система решений однородной СЛАУ.
47. Теорема о структуре общего решения неоднородной СЛАУ.
48. Площадь плоской фигуры в прямоугольной и полярной системах координат.
49. Длина дуги плоской кривой. Вычисление длины дуги в прямоугольной и полярной системах координат.
50. Вычисление объёма тела с помощью определённого интеграла.
51. Несобственные интегралы 1 рода.
52. Несобственные интегралы 2 рода.

Ответы: (скачать фото лекций архивом)

1. Определение вектора. Основные понятия. (назад)
   
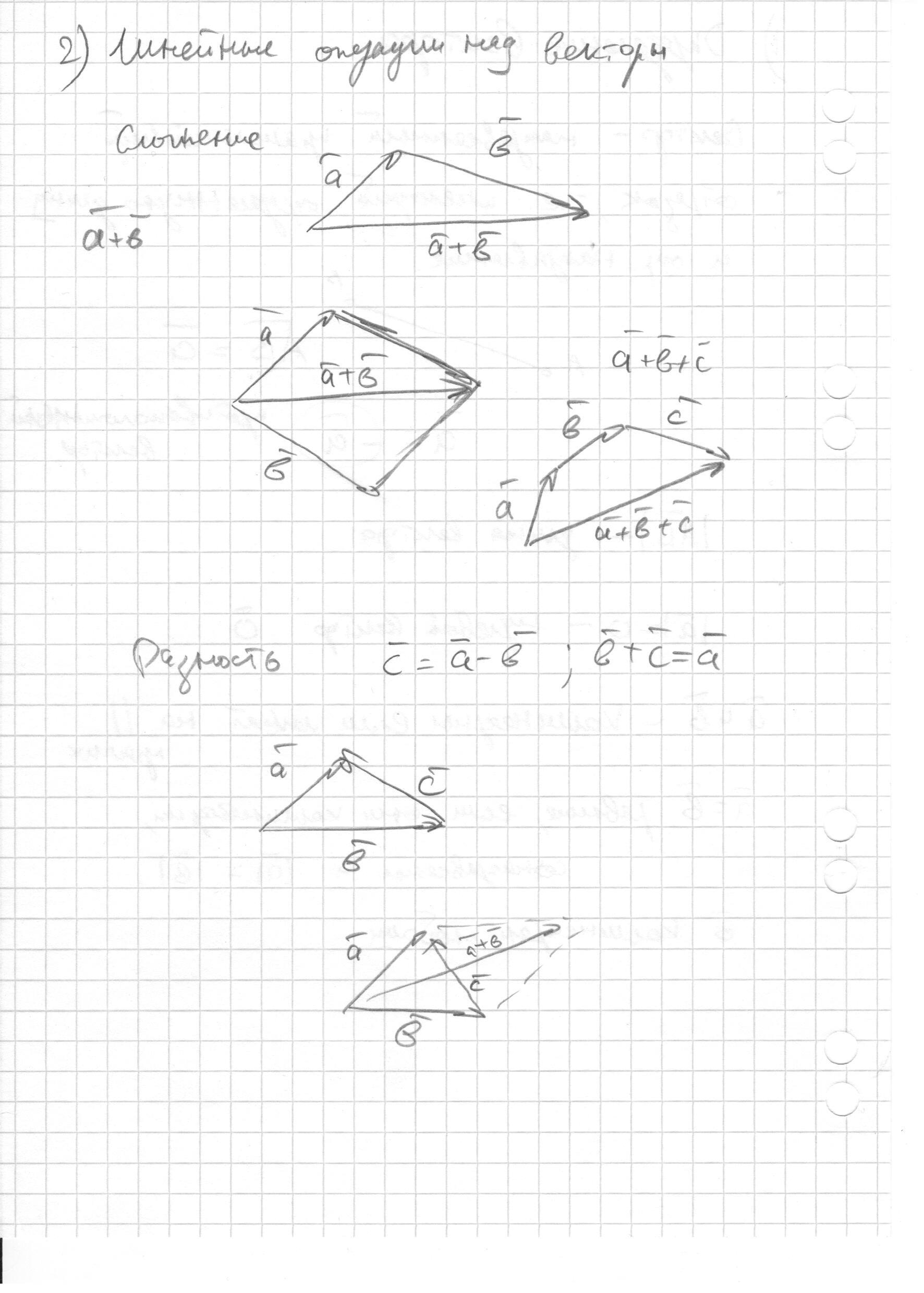
2. Линейные операции над векторами и их свойства. (назад)
   
   
3. Проекция вектора на ось. Основные свойства. (назад)
   
4. Линейная комбинация векторов. Понятие базиса на плоскости и в пространстве. (назад)
   
5. Понятие системы координат. Разложение вектора по ортам координатных осей. (назад)
   
   
6. Модуль вектора. Направляющие косинусы. (назад)
   
7. Действия над векторами, заданными своими координатами. (назад)
   
   
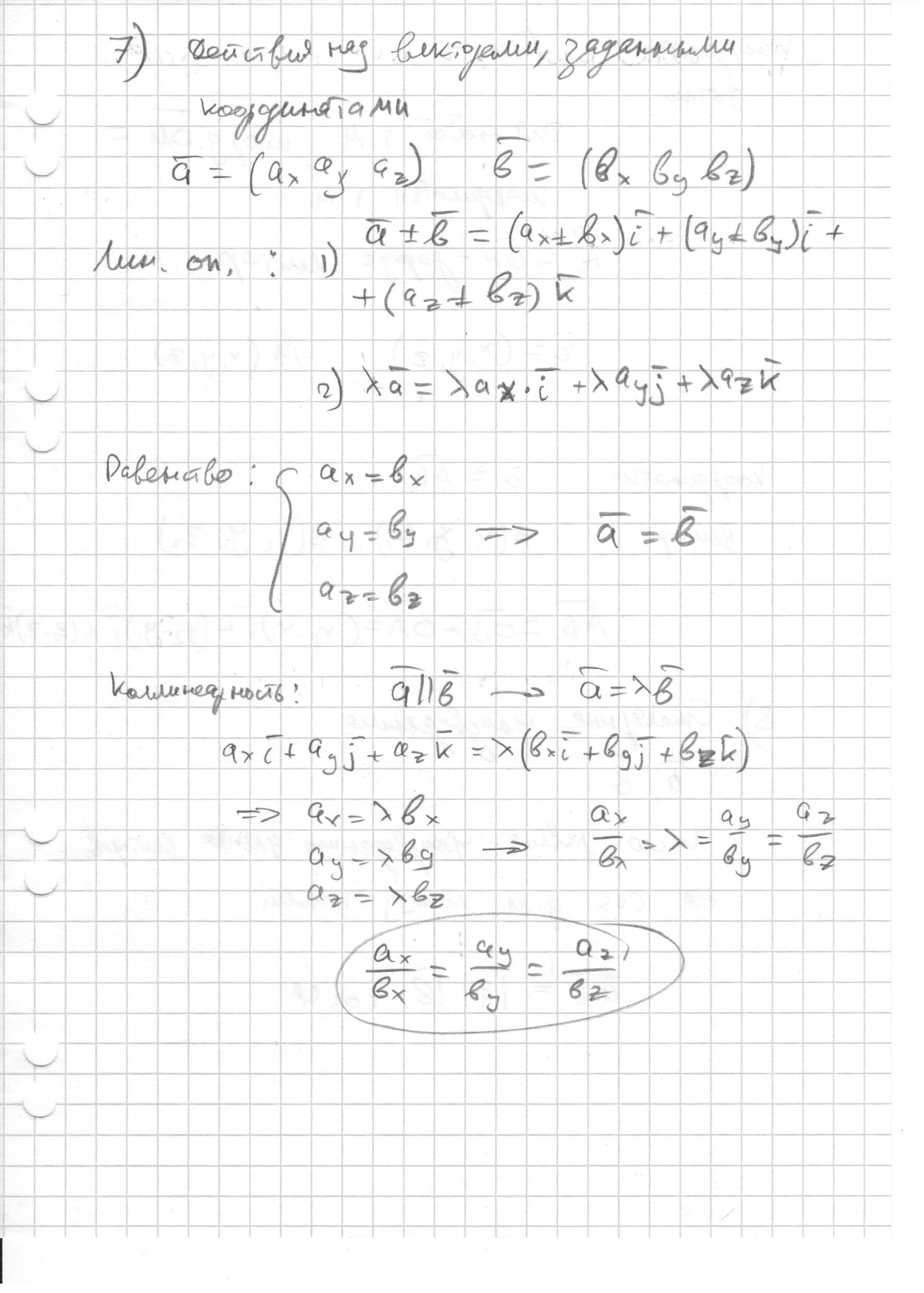
8. Скалярное произведение векторов. Определение и основные свойства. (назад)
   
   
9. Выражение скалярного произведения векторов через их координаты. (назад)
   
10. Векторное произведение двух векторов. Определение и основные свойства. (назад)
    
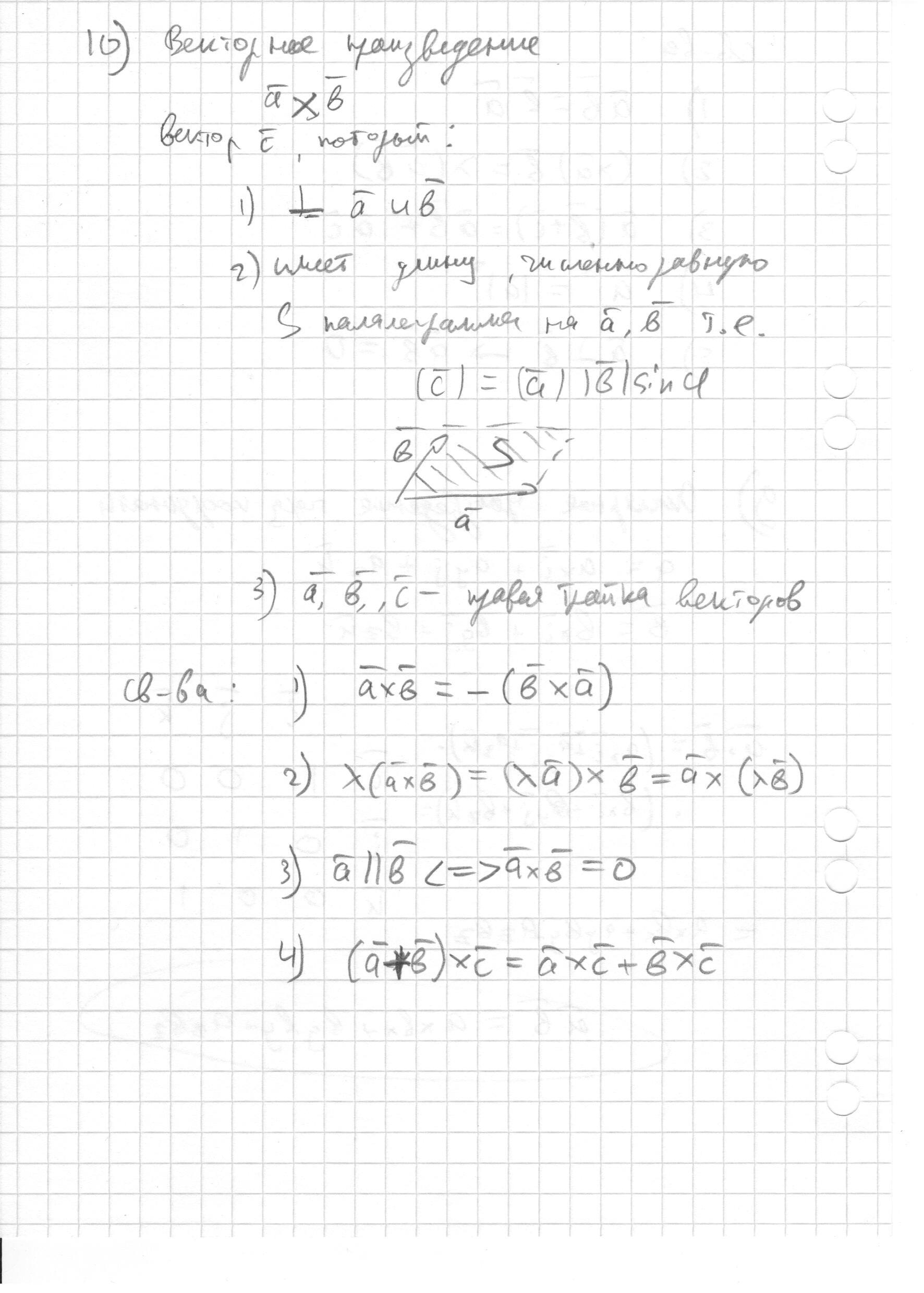
11. Выражение векторного произведения векторов через их координаты. (назад)
    
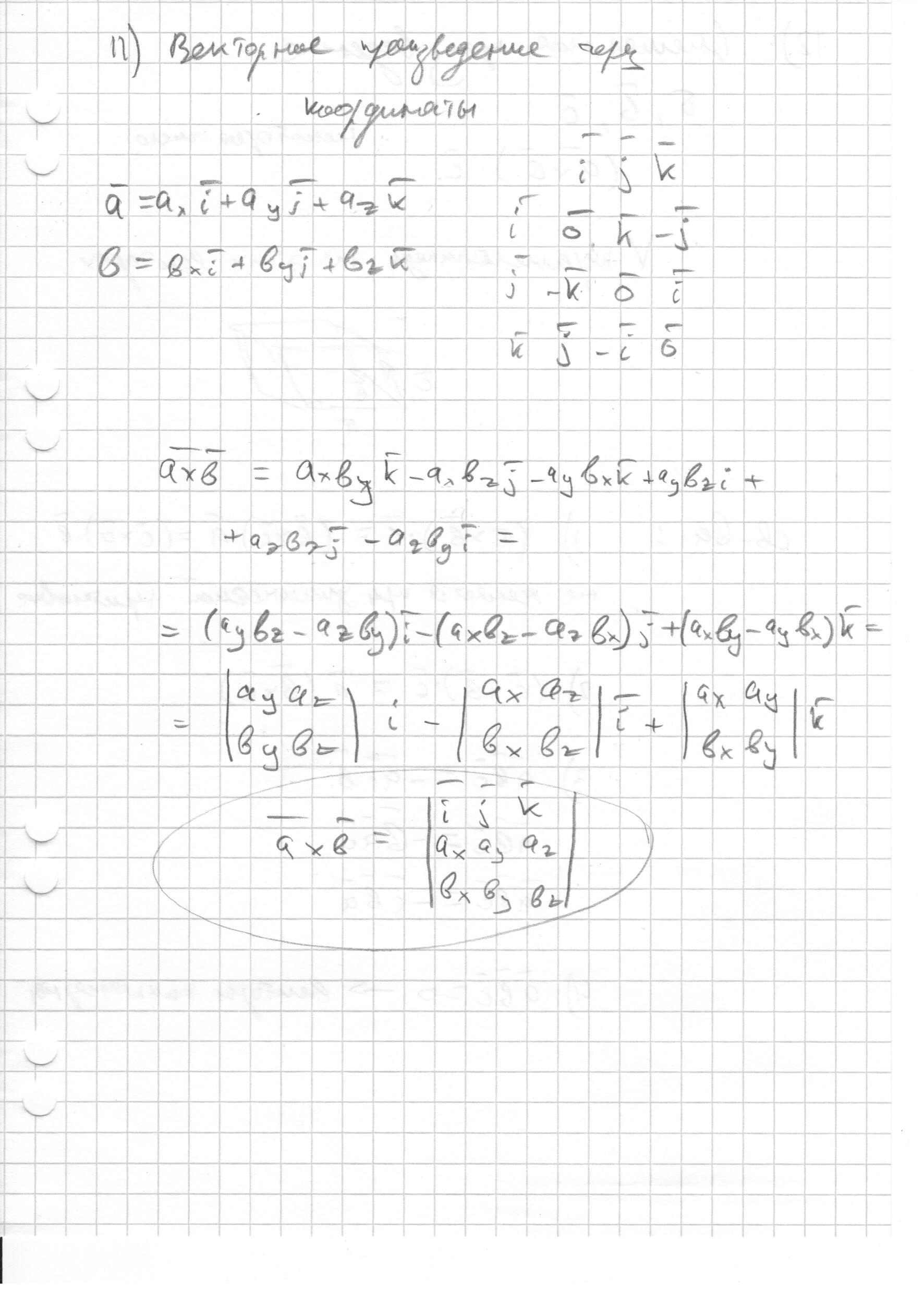
12. Смешанное произведение трех векторов. Определение и основные свойства. (назад)
    
13. Выражение смешанного произведения векторов через их координаты. (назад)
    
14. Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору. Общее уравнение плоскости. (назад)
    
    
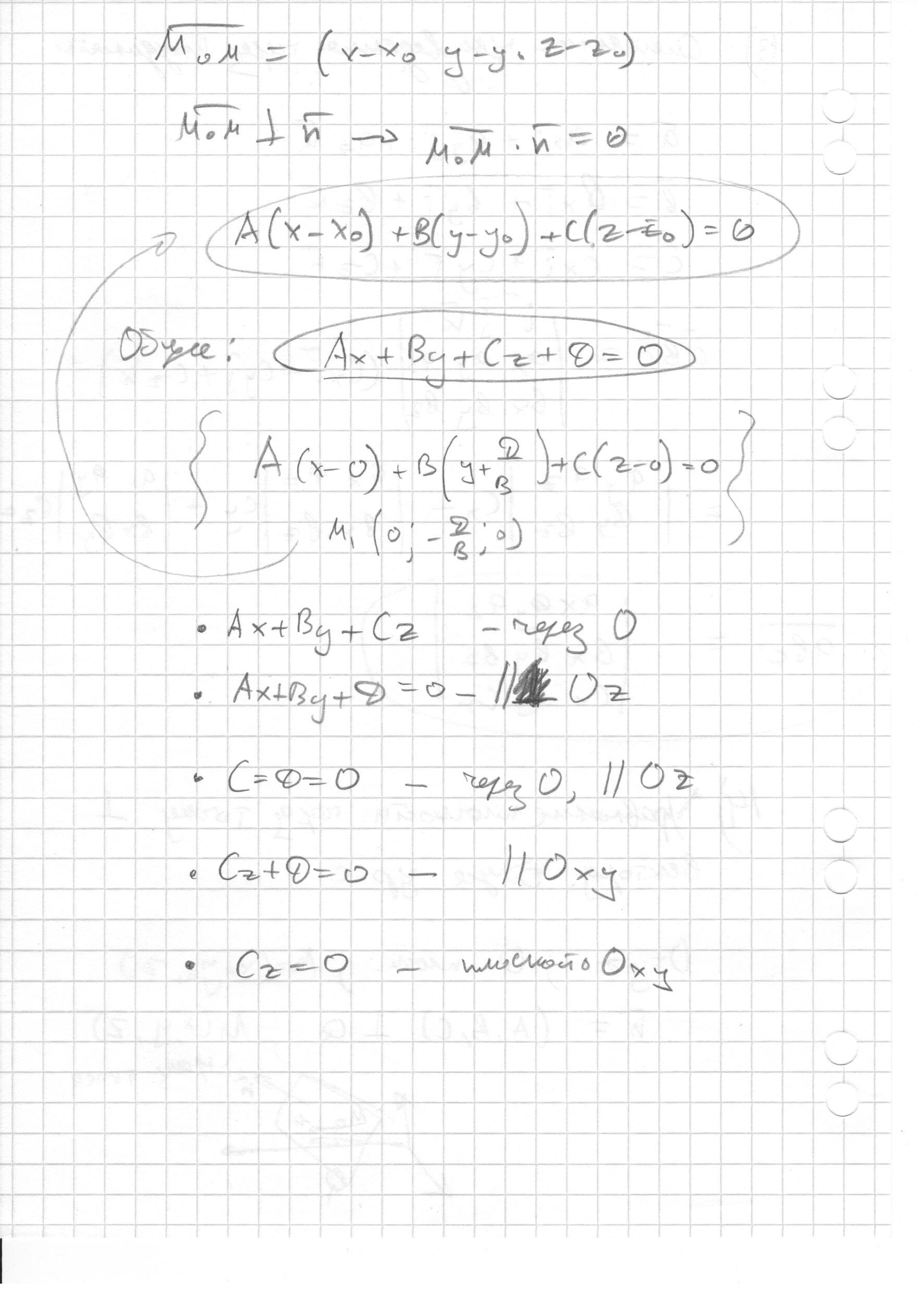
15. Уравнение плоскости, проходящей через три точки. (назад)
    
16. Уравнение плоскости в отрезках. Нормальное уравнение плоскости. Преобразование общего уравнения плоскости к нормальному виду. (назад)
    
    
17. Расстояние от точки до плоскости. (назад)
    
18. Угол между двумя плоскостями. Взаимное расположение двух плоскостей в пространстве. Уравнение пучка плоскостей. (назад)
    
    
19. Прямая в пространстве. Векторное уравнение прямой. Параметрические уравнения прямой. (назад)
    
20. Канонические уравнения прямой. Уравнения прямой, проходящей через две точки. (назад)
    
21. Общие уравнения прямой. Преобразование общих уравнений прямой к каноническому виду. (назад)
    
22. Угол между прямыми. Взаимное расположение прямых в пространстве. (назад)
    
    
23. Условие, при котором две прямые лежат в одной плоскости. (назад)
    
24. Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости. (назад)
    
    
25. Задача о вычислении координат точки пересечения прямой с плоскостью. (назад)
    
26. Условие принадлежности прямой плоскости. (назад)
    
27. Задача о вычислении расстояния от точки до прямой в пространстве. (назад)
    см. 26
28. Задача о вычислении кратчайшего расстояния между скрещивающимися прямыми в пространстве. (назад)
    
    
29. Эллипс. Определение, рисунок и основные понятия. (назад)
    
    
    
30. Гипербола. Определение, рисунок и основные понятия. (назад)
    
    
31. Парабола. Определение, рисунок и основные понятия. (назад)
    
32. Определители n-го порядка и их основные свойства. Минор и алгебраическое дополнение. (назад)
    
    
33. Матрица. Определение, основные виды матриц. (назад)
    
34. Линейные операции над матрицами и их основные свойства. (назад)
    
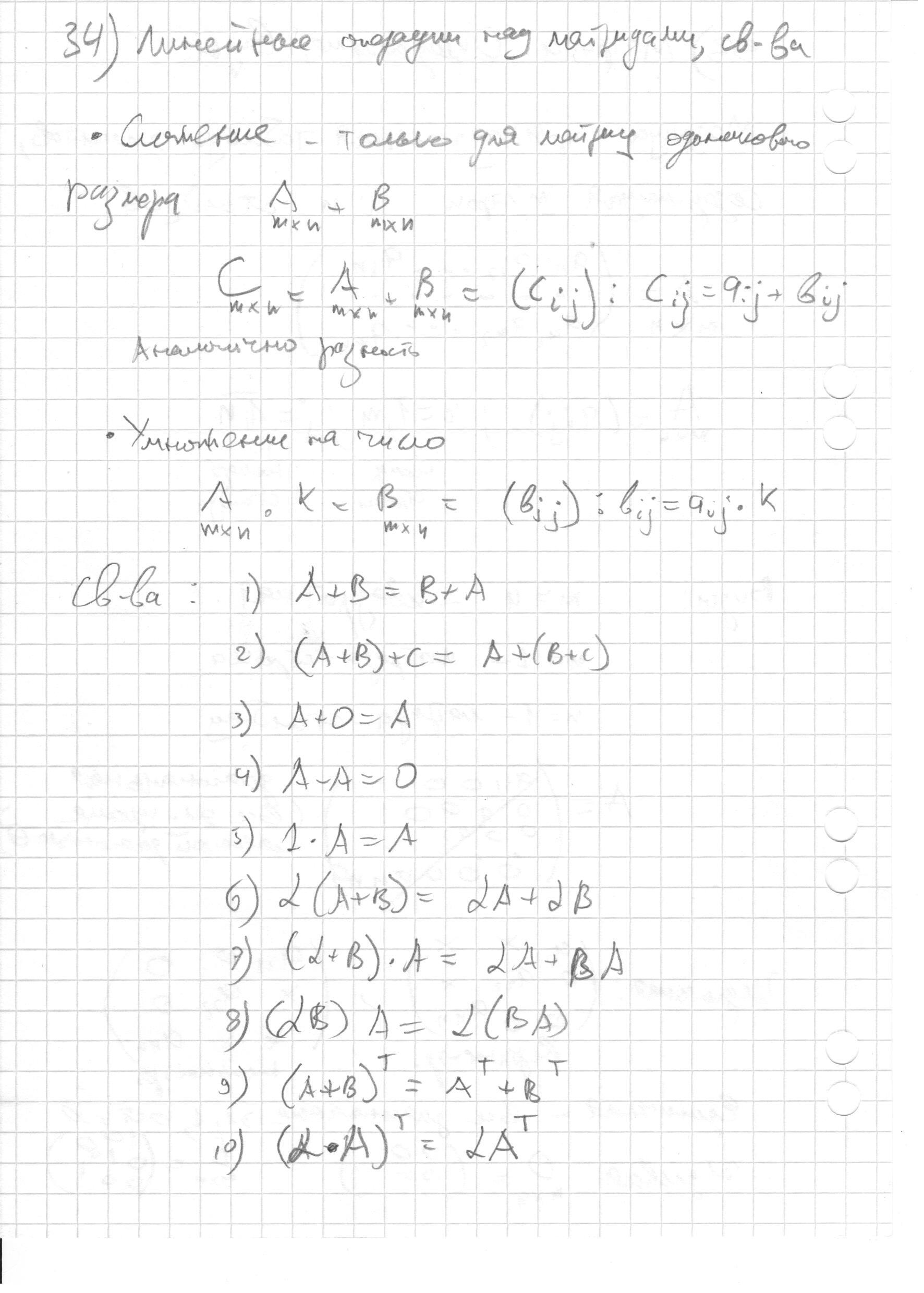
35. Произведение матриц. Определение и основные свойства. (назад)
    
36. Обратная матрица. Определение и основные свойства. (назад)
    
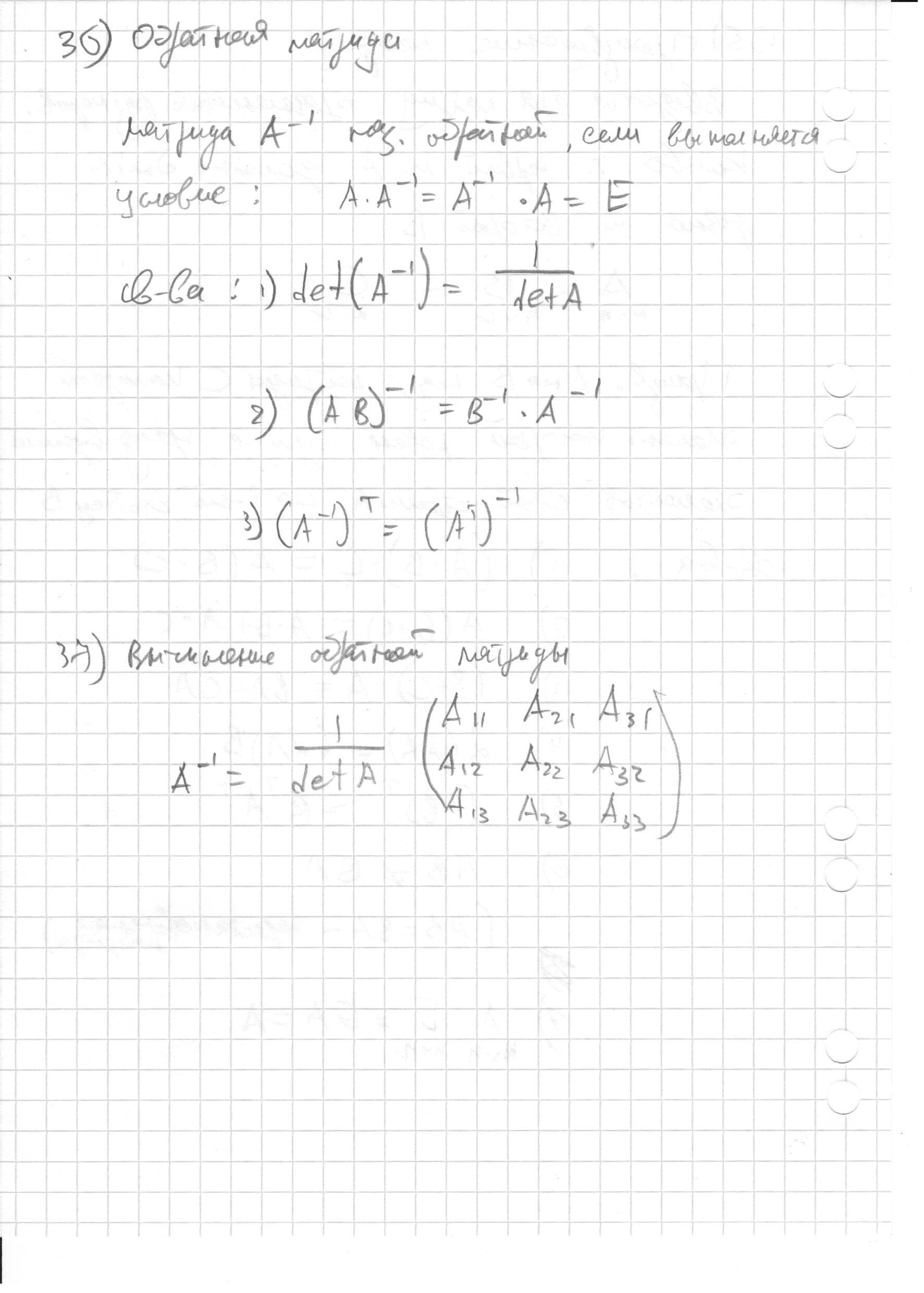
37. Вычисление обратной матрицы. (назад)
    см. 36
38. Решение СЛАУ с квадратной невырожденной матрицей коэффициентов с помощью формул Крамера. (назад)
    
39. Решение СЛАУ с квадратной невырожденной матрицей коэффициентов с помощью обратной матрицы. (назад)
    #Ранг матрицы. Элементарные преобразования матрицы.см. 40
40. Ранг матрицы. Элементарные преобразования матрицы. (назад)
    
    
41. Линейная зависимость системы столбцов. Основные теоремы об их линейной зависимости и независимости. (назад)
    
    
42. Теорема о ранге матрицы. (назад)
    см. 41
43. Теорема о базисном миноре. (назад)
    
44. Условие совместности и несовместности СЛАУ. Теорема Кронекера-Капелли. (назад)
    см. 43
45. Общее решение однородной СЛАУ, базисные и свободные неизвестные. (назад)
    
46. Фундаментальная система решений однородной СЛАУ. (назад)
    
47. Теорема о структуре общего решения неоднородной СЛАУ. (назад)
    см. 46
48. Площадь плоской фигуры в прямоугольной и полярной системах координат. (назад)
49. Длина дуги плоской кривой. Вычисление длины дуги в прямоугольной и полярной системах координат. (назад)
50. Вычисление объёма тела с помощью определённого интеграла. (назад)
51. Несобственные интегралы 1 рода. (назад)
52. Несобственные интегралы 2 рода. (назад)